A Mathematical Description of Markets

a working paper
©2008 Robert H. Rimmer

Introduction

This working paper develops some evolving thoughts on a description of market time series that are closely tied to observable data.  The goal is to extract as much information as possible from easily available data, developing a model that closely fits observation while adding some theory which appears consistent with the observations at hand.   Where assumptions are made they must be as simple as possible, and they should be subject to change as the system evolves.  The paper has links to the mathestate website which add to the description with Mathematica code to assist the analysis.  Comments are welcome.  Send email to mathestate@gmail.com.  Printable version in pdf format.

Price Time Series and Returns

The Figure [1] shows a typical time series of prices, of the SPY ETF.  The prices rise and fall over time.  Investors would like to know the return in the future, but they may have to accept from the outset that such knowledge is most likely not possible.  The goal of this presentation is to formulate ideas for modelling market behavior with quantitative methods which will aid in assessment of risk and reward in financial markets.

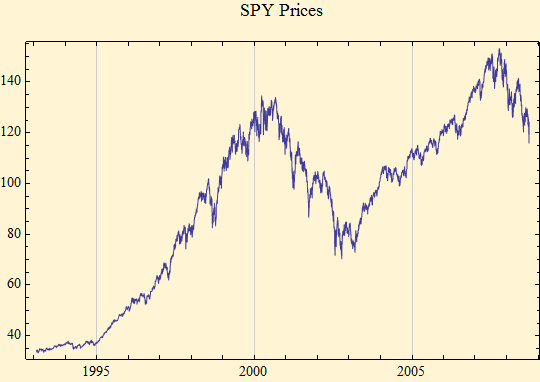
Figure [1]

The focus will be on the variation of price differences in the past, with the hope that analysis of this experience will yield measures of risk that can be extended into the future.  Logarithmic returns provide the most consistent basic measure of price differences because they are summable to generate interval log returns; if needed the time series can be reconstructed with the knowledge of the price at any one point in the log return time series.  Figure [2] shows a typical daily time series.

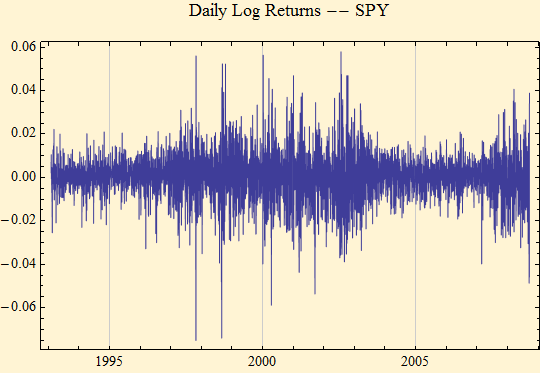
Figure [2]

Volatility in returns may be simply modelled with a moving average of the absolute value of the log returns.  Figure [3] suggests that volatility of the time series is not stationary and probably cannot be modeled with the assumption that there is a single statistical distribution from which the return data is drawn.  Figure [4] shows the same plot with a superimposed plot of a the moving average of the absolute value of a simulated normal variation of random data generated from the standard deviation and mean of the distribution of the sample log returns.

Figure [3]

Figure [4]

Such a stationary normal distribution is a common assumption in the financial literature, but it does not account for the extreme variation seen in market returns.  The absolute magnitude of the variation is simply much larger than range than allowed with the normal distribution assumption.  Market data have heavy-tails.  Additionally there is clearly change in of the magnitude of the variation with time -- suggesting that the distribution is not stationary.  If these observations are ignored and the distribution is presumed stationary and normal, Figure [5] shows the fit calculated from the standard deviation and mean of the log return sample with the assumption that the data are normally distributed.  The fit of the density to the data histogram is poor.

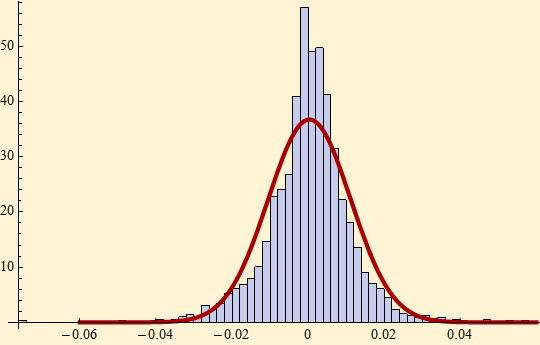
Figure [5]

A Jarque-Bera test on the data, shows the Jarque-Bera chi-square statistic followed by the probability that the sample is drawn from a normal distribution -- zero.

But the worst part of the assumption of a normal distribution is that the tails of a normal distribution taper very rapidly, so the normal assumption will exclude the possibility of extreme returns.  However, such events are frequently seen in financial markets.

Stable Distributions

There is a class  of distributions, called stable distributions, which may have of heavy tails.  The class derives its name from the property that the shape of the distribution is unchanged (stable) if random variables from the distribution are summed.  The normal distribution also has this property and it belongs to the class of stable distributions, but its tails are light.  All other members of the class have heavier tails ranging from slightly heavier than to normal to extreme.  Mandelbrot in 1963, suggested this class of distributions for certain financial data after studying the returns from cotton prices over a century.  Mandelbrot knew that successive price changes did not appear to be independent and that price time series did not look like it was stationary, but he argued that the large instantaneous price changes and infinite variance permitted by stable distributions could account for the appearance of non-stationarity and further that the patterns of dependence might have a large probability of occurring by chance in the setting of stable distributions.

Stable distributions, although attractive in theory, are difficult to calculate.  There are only three members of the class with simple formulae for their densities, the normal, Cauchy, and Levy distributions.  They are shown below, plotted with the same scale factor.  The normal distribution in blue is symmetric and has light tails; it is the only stable distribution for which variance or the second moment exists.  The Cauchy distribution in red is also symmetric, but has tails that are so heavy that no expectation or mean exists for the distribution.  The Levy distribution in gold, likewise has no expectation and is totally skewed.

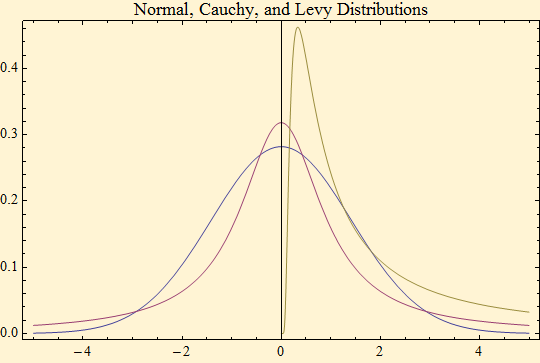
Figure [6]

The difficulty in accurately calculating the general case was overcome with faster computers and a numerical integration algorithm by Nolan in the 1990s.  Figure [7] shows a few general stable distribution densities with tail exponents greater than the Cauchy distribution (expectation exists, but variance does not).

Figure [7]

With the ability to compute stable distributions, we can fit our log return data to a stable distribution.  Figure [8] shows that the fit is much better than that of the normal distribution, along with the stable parameters, {α, β, γ, δ}.

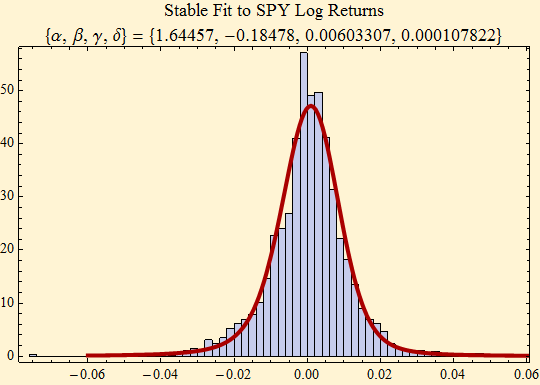
Figure [8]

Presently there is no good method to determine whether a sample is drawn from a stable distribution.  On a log-log plot of the distribution function, the tails of a stable distribution become linear with the slope given by the shape parameter, α.  Figure [9], below, shows a log-log fit to the cumulative distribution function.   To align the tails, the absolute value of the left tail is shown in blue; the right tail is shown as 1- probability in red.  In this format stable distributions with α < 2, show linear parallel tails with the slope of minus α.  If β is zero the tails are superimposed (when β = ±1, the lighter tail is not linear).  The tail of a Normal distribution calculated from the sample is shown in green and is not linear.  The dots show the data points of the respective tails.

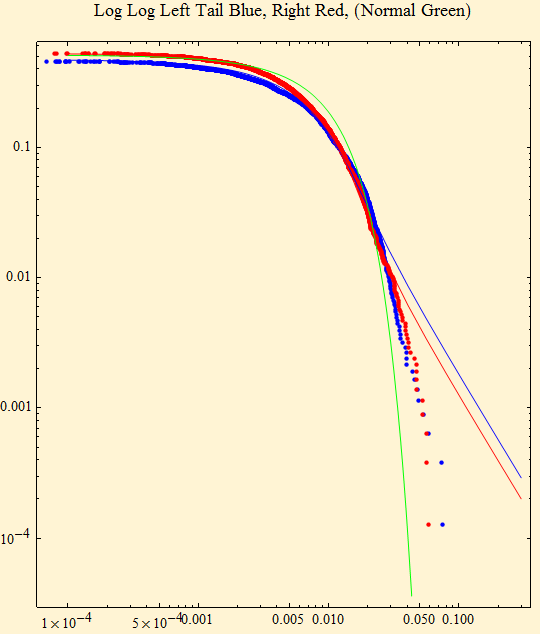
Figure [9]

Figure [9] presents a huge problem mathematically.  Although the tails of the data are heavier than a normal distribution and are nearly linear, they are not heavy enough to obey stable laws.  Calculation of the tail exponents, Figure [10], shows that the tail exponents are high enough (light enough) that sums of random variables from such a power tail distribution will converge to a normal distribution, by the central limit theorem.  For most researchers this is the end of the story: financial returns are not from stable distributions.

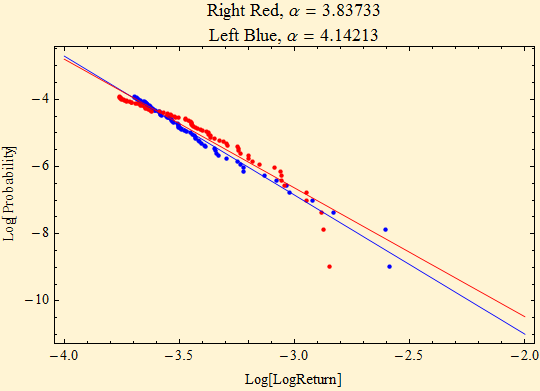
Figure [10]

Non-Stationary Distributions

All of the data analysis in the previous section was based on a bad assumption, namely that financial time-series are stationary.  Even with the assumption the data seem to suggest that a stable model is more likely than a normally distributed model, because of the frequency of extreme events seem in financial markets.  Figure [11] displays an autocorrelation function of the volatility modeled as the absolute value of log returns.  The graph shows that autocorrelation persists for up to a hundred day lag in the data.  This indicates a non-random structure to volatility, even though it is hard to show persistent autocorrelation in the raw log return data.

Figure [11]

So the data are not completely random.  There is a structure of serial dependence in volatility as measured by absolute value of logarithmic returns.  Stable distributions have the mathematical property that the absolute mean deviation of a sample from a stable distribution with given parameters {α, β, γ, δ}, is proportional to the scale factor, γ.  Figure [12] shows a plot of the estimate of gamma for a moving look back over the previous 30 days.  Using such a small sample, leads to high probability of error in the estimate, nevertheless, the plot is strikingly similar to the moving average of the absolute value of log returns.

Figure [12]

When the data are rescaled by simply dividing by this estimate of gamma, the pattern of serial dependence in the autocorrelation function seems to disappear, Figure [13].

Figure [13]

Figure [14] shows the stable fit to the rescaled data.  The tail exponent of the data points is now consistent with stable behavior.  This is not a proof!  But the data do seem to fit a model of a non-stationary stable distribution, with the major change over time being due to the scale factor.  

Figure [14]

Here is a hypothesis of how such a model could arise.  In markets structured by a continuous double auction, market orders and limit orders are constantly flowing into the system.  When equal numbers of market buy and sell orders arrive in a small finite interval they are matched at the last price.  If there is an excess of buy or sell market orders, then they are matched against the orders in the sell or buy limit order books and the price changes.  The magnitude of the change is dependent on the structure of the limit order books.  This is an area in need of more research, but some investigations into the limit order books have suggested that they do lead to heavy tailed returns.  By the generalized central limit theorem, sums of random variables from power tail distributions having a tail exponent less than two will converge to stable distributions.  It is also not hard to imagine that the structure of the limit order books will not be static, but will immediately respond to market conditions.  If the scaling is the major response to changes in the markets, then a model of stable random noise with amplitude modulation, may be a reasonable starting structure.  Almost certainly things are more complicated, but more research into the mathematics of a non-stationary stable model may lead to useful results.

The structure of the volatility parameter, γ, is interesting.  Although there is a strong pattern of serial dependence in the data, a histogram of the data is nicely fit by the lognormal distribution.  This phenomenon suggests that a statistical distribution might be designed for market data as a distribution arising from the product of a lognormal random variable and a stable random variable.  A lognormally scaled stable distribution has been created.

High Resolution Data

We have been collecting minute by minute price data on the SPY ETF for more than a year.  These data allow us to take the above ideas further without having to estimate volatility over long periods of time.  Rather, we can estimate the stable gamma from each day's logarithmic price changes; there is no time lag in the estimate.  Figure [15] shows the closing daily price of SPY and the calculated stable scale factor, gamma, for each day from the minute by minute intra-day log returns.

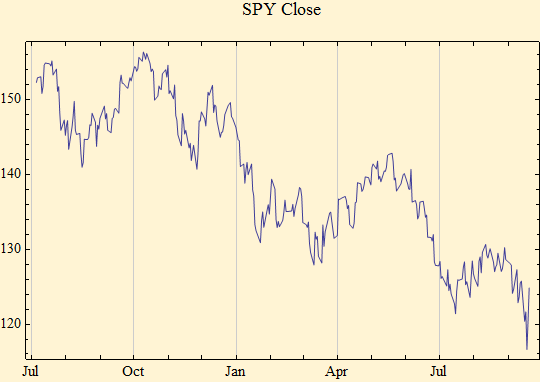
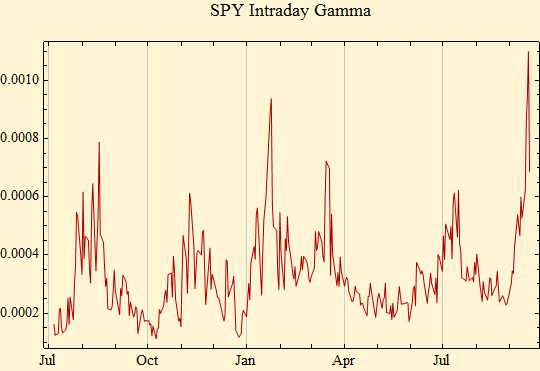
Figure [15]

An inverse relationship in the trend of volatility and the trend of market price is apparent.  Figure [16] shows the trend of daily volume over the same time frame.

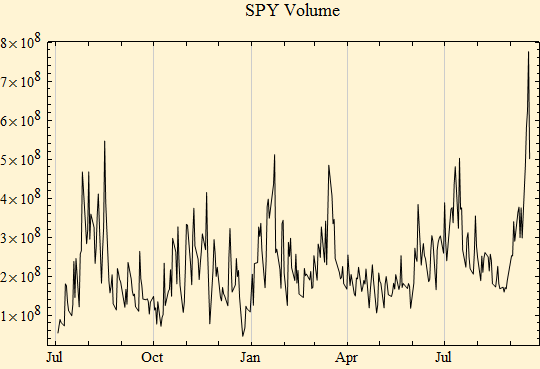
Figure [16]

Clearly volatility is related to volume.  Over longer time frames this relationship is not so tight as volume appears to be rising over time and the market's capacity to handle volume is increasing over time.  Thus volatility amplitude changes in the past would be associated with lower magnitude of volume than they are today.

It seems possible to begin to draw some conclusions from the pictures above.

1. The trends of prices and volatility are inversely related.
    
2. For short periods of time--as a year--volatility and volume are closely related. Over long periods of time this relationship is less clear because volume seems to have an independent time related growth rate.

3. Peaks of volatility form more quickly than volatility decays.  There seems to be cyclic behavior, but the occurrence of the peaks is not likely predictable.

4. The magnitude of the valleys of the volatility (stable gamma) still is rising. We imagine that we will have to see a lower valley, before we can believe that there is a decreasing trend in volatility. The market peak last October occurred at the lowest valley in volatility in recent data.

Figure [17] shows that if we adjust out the daily volatility, by dividing each day's data by the average daily scale factor we get very close to a stable model, particularly in the tail behavior of the log-log distribution fit.  The wiggle in the tails can be accounted for by the intra-day cycle of higher volume and volatility during the hours near to the market open and close.  For more details on these phenomena see the Market Data page.

α	β	γ	δ
1.79476	0.0151728	1.0151	-0.00171327

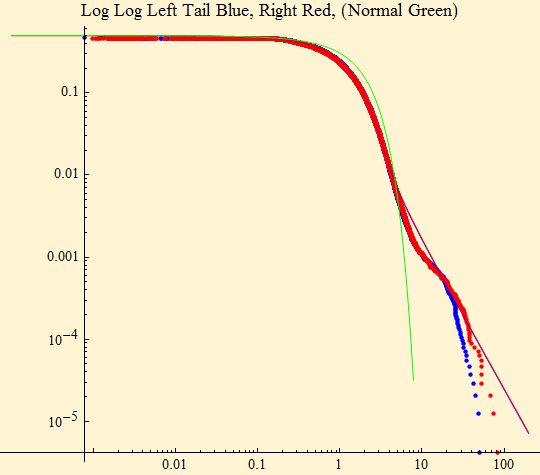
Figure [17]

We now generate two new hypotheses.

1.  Almost all the information, statistically non-random behavior, economists' "rational" behavior, in the market time series is contained in the volatility curve, which is well represented by a non-stationary stable γ parameter. When this is adjusted out, what remains is a stable random model.

2.  The volatility curve can be predicted by runs, of volume. High volume increases the probability of mismatched market buy and sell orders, causing deeper excursions into the limit order books of the continuous double auction; this causes the changes in volatility. That is: herd behavior causes the volatility. Investors are not logically rational, rather they behave like the parable of the Norwegian lemmings.

If the above ideas are correct, then we can make predictions from the daily volatility measurements. The extreme returns plot, Figure [18], clearly shows that markets rise more consistently when extreme returns are less frequent.  The red dots show the extreme returns outside the quantile range [0.02, 0.98], return scale on the right.

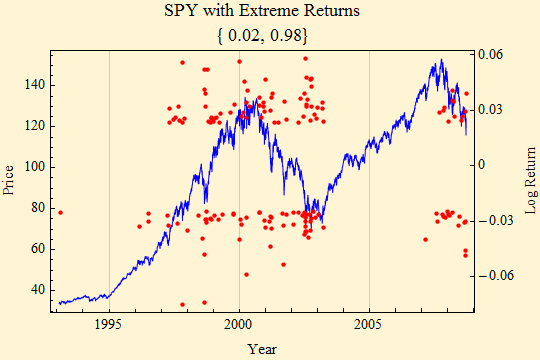
Figure [18]

References

Bouchaud, M. and Potters, Theory Financial Risk and Derivative Pricing, Cambridge, 2003.

B. B. Mandelbrot, Fractals and Scaling in Finance: Discontinuity, Concentration, Risk, New York: Springer-Verlag, 1997.

J. P. Nolan, Numerical Calculation of Stable Densities and Distribution Functions, Communications in Statistics-Stochastic Models, 13(4), 1997 pp. 759–774.

Plerou, V., Gopikrishnan, P., Amaral, L., Meyer, M., Stanley, H.E. (1999) Scaling of the distribution of price fluctuations of individual companies. Physical Review E,  60:6

Smith, E., Farmer, J.D., Gillemot, L., Krishnamurthy, S., Statistical theory of the continuous double auction, Quantitative Finance, 3, 481-514. Farmer's web site has many useful references.

© Copyright 2008 Robert H. Rimmer  Sat 20 Sep 2008