LogarithmicReturns

Why Use Logarithmic Returns?

The question in the title has been one of the most common queries leading visitors to this site. The current page is a more direct attempt to answer the question while simultaneously showing how logarithmic returns work.

When making an investment it is natural to wonder what the investment will be worth in the future. A simple bank account paying compound interest provides a model to explore the concept of logarithmic return.

A starting principal is which grows at constant annual decimal rate, ar, with interest compounded each year. The resulting formula, has time, t, in years. P is the principal at time t .

More typically for a savings account, the compounding interval might be daily with the formula becoming:

To arrive at the above formula the annual rate ar annual rate is divided by the number of days in a year to give a simple daily rate; in doing this the actual annual return in a year's time will be larger than the starting annual rate. The effective annual rate will be:

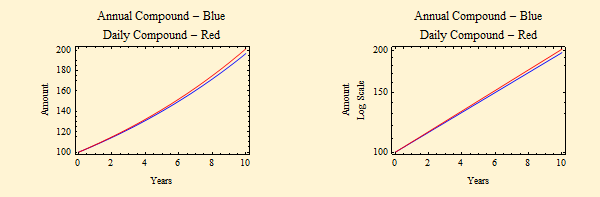
The difference in the return between a simple 7% annual return on an investment of $100 and that annual rate divided by 365 with daily compounding is shown in the graphs below. The plot to the left is on a linear scale and the plot on the right has a logarithmic scale for the accumulated principal amount. Note that on the log amount scale this is a linear problem, with the formula:

There is no reason to limit the compounding interval to days, the compounding interval can be made infinitely small leading to the formula for continuous interest. r is now a continuous logarithmic rate and e is the base of natural logarithms.

This formula can be solved by taking logarithms to get the logarithmic rate, r.

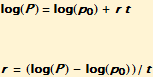
Now suppose that we have a sequence of prices each at the same interval of time apart, let's assume the unit difference here is one day.

The log prices are

The log returns of this series are simply the sequential differences of log prices at a unit interval, in our example daily.

or equivalently.

The sum of the series of returns now is the same as the return over the whole interval since all but the first and last log prices cancel out:

The average return over all the prices becomes:

So here we have a simple answer to the question, why use logarithmic returns? By using log prices we can convert an exponential problem to a linear problem. Logarithmic returns are simply first differences of log prices sampled at the same unit time interval. Sums of logarithmic returns over a time interval, give the logarithmic return for that interval, and a mean return can be calculated by dividing that interval by the number of time units in the interval.

Note that the mean log return of a time series of prices is determined by only three numbers, the starting price, the last price and the number of time intervals between the prices. This is true even if the series consisted of thousands of returns. This "expected" return thus gives no information about what happened over the sub intervals. On a log price plot this is the same as determining the rate by fitting the price series by drawing a line through the first and last prices. When you are quoted a historical return you usually are given this result converted to an annual decimal return.

Decimal returns, or on multiplying by 100, percent returns, do not have such a simple structure.

All the denominators are different so this method has a problem that the returns cannot be easily added or subtracted. And the returns are not symmetric, i.e. if one starts with a fixed amount and one day has a return of -0.01 and the next day have a return of +0.01, the initial value of the investment has not been regained. Logarithmic returns can be simply added. From here on log will be considered the natural logarithm to the base e.

A typical investment problem is more complicated than a bank account. We have a series of prices, and the return is unknown and variable. By using logarithmic returns (the first differences of log prices sampled at a specific interval), we can break the problem down into one that is linear, based on an expectation of continuously compounded return. Further if we find that the logarithmic returns (log returns) behave like random variables, then sums of such random variables will obey the mathematical laws of stable distributions. Unfortunately life isn't that simple.