Hitting Time

A hitting time or stopping time of a stochastic process is needed to calculate option prices for a stock or the probability that limit order will be executed.  For markets, typically a smooth stationary stochastic process such as Brownian motion is assumed, and stochastic calculus is used to calculate the results.  We have shown that distributions of market returns are probably not stationary so it is unlikely that such a strategy will work for pricing options or calculating stopping times.  But even if the distribution of returns were stationary, it is not clear that hitting times can be calculated from heavy-tailed distributions using stochastic calculus.

We show why by example.  Suppose we want to know the probability for execution of a limit order entered for a stock.  We will take the example of the SPY for which we have calculated parameters on other pages.  We will assume the following adjusted stable parameters {α, β, γ, δ} for minute by minute trading data.

Stable parameters
{1.792, 0.00729, 0.0002696, 6.866667526673047e-7}

Suppose the current price for SPY is 143.00 and we want to calculate the probability of execution of an order within one month to sell at 156.00.  We can do this by simulation, using the stable random generator to generate minute by minute returns and accumulate their sums.  We will run enough trials to estimate probability for the event which will be a cumulative log return greater than Log[156./143.]:

0.0870114

We will assume that the variation on a minute by minute basis will divide the returns finely enough that we will closely approximate the time of execution within a few minutes.  Using stable distributions and their scaling properties, we can calculate the probability that the sum of log returns will be greater than the limit we have set at the end of 21 trading days or about one month:

0.0906372

But this does not include the probability that the cumulative sum may have risen above our limit and then fallen again by the end of a month, thus we feel that the probability of execution should be higher than 0.09.

Here is the hitting time algorithm in Mathematica.  This will generate one run of n sums of random variables.  The algorithm puts out the whole set of accumulated sums if the trial results in a success and an empty set if there is no hit.

We run a five hundred trials over 21 days with 391 one minute trading intervals each.

The probability of a hit is calculated as the number of hits/500, and as we suspected it is higher than the 0.09 that we estimated from the scaled parameters.  To achieve a precise estimate, tens of thousands of trials need to be run.

Here is a plot showing all the successful runs.  Many of the hits occurred because there was at least one wild jump in the price.  We do not believe that the methods of differential stochastic calculus will work very well in this situation, because the integrals will not be smooth.  The situation becomes even more impossible if the scale factor is moving.

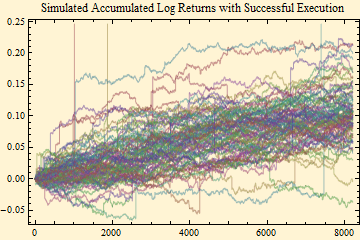
Below is a histogram of the hitting times of the successful trials.  Remember that most of the trials failed.  Even though we had a rather high sell price relative to the current price in the example, with a stable distribution as the model, there were a surprising number of hits within just a few days.

We have shown that we can by simulation estimate hitting times, but even at a one minute interval there are wild jumps under a stable regime with a tail exponent as high as 1.79.  The usual methods of stochastic calculus assume that the integration will be a smooth process; this is not the case for stable distributions.  Download the notebook and run larger trial sizes for better estimates, but exclude the plotting of the successful trials as it will take too long.

© Copyright 2008 mathestate    Fri 30 May 2008