LNN Random Variables

LNN random variables are simply generated.  We take the product of a Normal[ 0, ] and a LogNormal[ log(γ), σ] and add δ, the location parameter and expectation.  The in place of the usual normal standard deviation, changes the scaling to the same scaling as stable distributions.  We have chosen this because we have a method to estimate the scale factor for any stable distribution and it happens also to work reasonably for the LNN distribution, where the standard deviation does not because of the LNN's heavy tails.  Our Mathematica package has a function LNNRV which will generate the random variables.  Below is a histogram and the fit for 10,000 LNN random variables with parameters, {γ, σ, δ} = { 0.01, 0.4, 0.0003}.

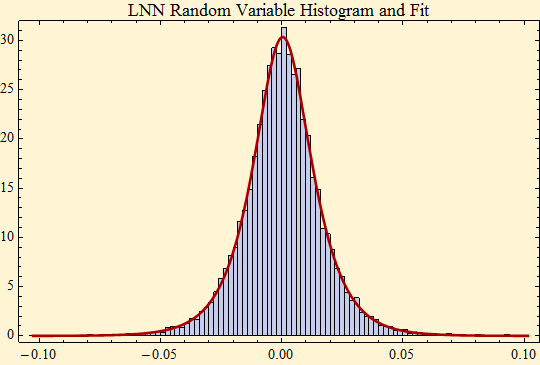
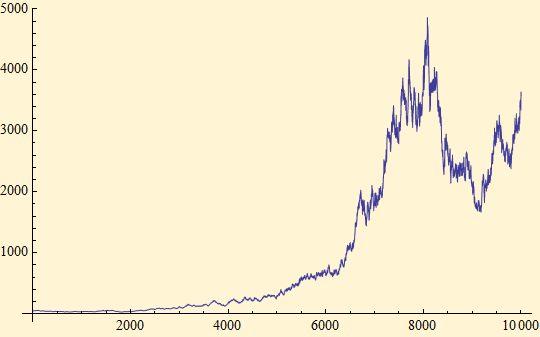
We chose the parameters to be typical of those of a large cap U.S. Stock.  Below is a price simulation equivalent to 40 years of daily data.  Since the tail fits of market data to this distribution are more accurate than the fits to a stable distribution, we believe that long run simulations will be more realistic.

On the next page in this series we explore parameter fitting.

© Copyright 2008 mathestate    Wed 18 Jun 2008