Generalized Extreme Value Distribution

The generalized extreme value distribution in standardized form is given below.

This function has a limit at ξ = 0, so it is continuous over the entire range of ξ.

A three parameter form of the distribution is needed for fitting, where μ is the location parameter and σ > 0 is the scale parameter, by substituting.

The full parameterization of the distribution function :

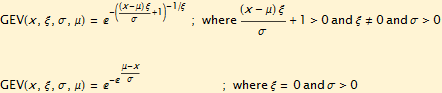
The density function is.

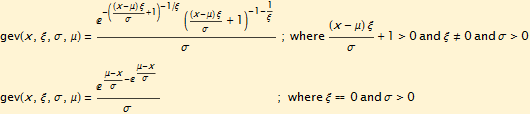
For maximum likelihood fitting, the corresponding log densities have an explicit form with the same corresponding parameter restrictions:

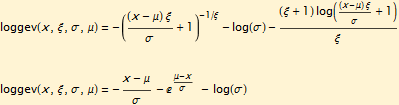
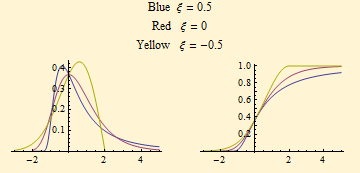
The plots of the density and distribution functions are shown below for the standardized distributions (σ = 1, μ = 0).  Note that the right tail of the yellow curve is abruptly truncated at x = 2.

These distributions form the limiting distributions of maximum or minimum values of a set of random variables from a stationary distribution.  The convergence is analogous to the convergence of sums of random variables by the generalized central limit theorem.  The maximum, , of a set of random variables is defined below.

For a minimum, , of a set the definition would be as shown below so the result would also be skewed positively.

With this definition in mind if,

then the limiting distribution for appropriately shifted and scaled x would be

For example assume the primary distribution is an exponential distribution with the distribution function,

where x is appropriately scaled and shifted,

We conclude that the limiting distribution for maxima of an exponential distribution has the form of the extreme value distribution such that ξ = 0.  The normal distribution and lognormal distributions also have extreme value distributions with ξ = 0, but since the lognormal distribution has a heavier tail it will require larger n to show convergence.

Next we take the case of the Pareto distribution function for x,

x>k

We scale and shift by

We conclude the extreme value distribution has the form,   Since stable distributions, with 0 < α < 2, and β ≠ ± 1, have asymptotically Pareto tails, we expect them to also converge to a generalized extreme value distribution with ξ = .

For further discussion of classes of extreme value distributions see:
McNeil, A.J., Frey, R., Embrechts, P. Quantitative Risk Management, Concepts, Techniques, Tools, Princeton University Press 2005, Chapter 7.

© Copyright 2008 mathestate    Fri 10 Oct 2008